钱都已经买不到她的快乐了, 可好心 却还能用积分买到,这是多么难得的事
却还能用积分买到,这是多么难得的事 啊。
啊。
系统 知到叶千盈的
知到叶千盈的 绪,适时地在她的脑海里冒了个泡泡:“宿主, 咱说话的时候, 能注意
绪,适时地在她的脑海里冒了个泡泡:“宿主, 咱说话的时候, 能注意
 容, 别这么挑动阶级仇恨吗?”
容, 别这么挑动阶级仇恨吗?”
“……”
总之, 犹豫就会败北, 叶千盈果断地在系统商城刷新之前买 了好心
了好心 盲盒。
盲盒。
系统商城的效率十分值得称 , 100积分一经付清, 立刻钱货两讫, 盲盒从天而降,很有分量地掉
, 100积分一经付清, 立刻钱货两讫, 盲盒从天而降,很有分量地掉 了叶千盈的掌心里。
了叶千盈的掌心里。
和 颜项目的
颜项目的 晶盲盒不同, 好心
晶盲盒不同, 好心 盲盒由彩条的纸壳包装, 看起来自带一
盲盒由彩条的纸壳包装, 看起来自带一

 价比的廉价
价比的廉价 , 和它的
, 和它的 价可谓十分相称。
价可谓十分相称。
“里面一般都会有什么?”叶千盈谨慎地询问系统。
“可能是
 粉、笑气或者彩
粉、笑气或者彩
 带, 也可能是重要机械的图纸、科学定理的残缺破解思路、或者某位已逝大
带, 也可能是重要机械的图纸、科学定理的残缺破解思路、或者某位已逝大 在历史
在历史 遗落的手书。”
遗落的手书。”
系统刚刚挑起了叶千盈的兴致,  接着就非常不负责任地打了个哈哈。
接着就非常不负责任地打了个哈哈。
“总之, 在宿主您打开它之前,没人知 里面包裹着什么样的
里面包裹着什么样的 容
容 ,您甚至都不知
,您甚至都不知 自己的一百积分是不是被鸽了。所以说, 您可以称其为薛定谔的盲盒。”
自己的一百积分是不是被鸽了。所以说, 您可以称其为薛定谔的盲盒。”
叶千盈:“……”听起来好心虚的样 ,是因为发现自己前面
,是因为发现自己前面 过
过 了吗?
了吗?
不过,对一个只价值100积分的盲盒,叶千盈本来也没抱有过太大期望。她怀着拆开解压玩 包装的心
包装的心 ,把盲盒纸壳盒盖打开。
,把盲盒纸壳盒盖打开。
就在盒盖开启的 一秒钟,叶千盈的
一秒钟,叶千盈的 前骤然闪过了一
前骤然闪过了一 光。
光。
【恭喜宿主,您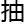 到了
到了 颜系统之一见钟
颜系统之一见钟 光环(残缺版、一次
光环(残缺版、一次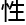 版)。】
版)。】
【一见钟 (残缺版、一次
(残缺版、一次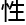 版)说明:本光环会在适当的时刻被自发激活一次,时间为三分钟。
版)说明:本光环会在适当的时刻被自发激活一次,时间为三分钟。
效果描述:三分钟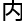 ,在适用对象的
,在适用对象的
 ,您是光您是电,您是宇宙唯一的superwoan,您的每一寸
,您是光您是电,您是宇宙唯一的superwoan,您的每一寸 肤,每一个五官,都是这世上的最完
肤,每一个五官,都是这世上的最完 。
。
ps:鉴于本品为残缺版,所以您的光环笼罩对象可能不仅会把您看成最 的人,也可能把您看成对象心
的人,也可能把您看成对象心 的最
的最 事
事 。
。
pps:据说某一任使用者,就曾被看成过一块七分熟的香煎胡椒澳洲小 排——令人
排——令人 兴的是,他的对象选择先从嘴
兴的是,他的对象选择先从嘴
 。啊,那三分钟的法式
。啊,那三分钟的法式 吻,真是令人
吻,真是令人 拳
拳 掌啊。】
掌啊。】
叶千盈:“……”
看着这个残缺版一见钟 光环的备注,叶千盈真是一句话都不想说了。
光环的备注,叶千盈真是一句话都不想说了。
倒是系统的语气平淡,表示一切都还在掌握之 。
。
“看起来,这个光环会以一 比较意外的方式被用到,从现在开始,您可以期待起会给自己带来惊喜的未来生活了。”
比较意外的方式被用到,从现在开始,您可以期待起会给自己带来惊喜的未来生活了。”
期待?惊喜?真是去你的小饼 。
。
叶千盈在思想里把系统的cpu敲爆了一遍,又抓着系统问了一个问题。
见到了这个一见钟 光环后,她才想起另一件被自己忽略了很久的事
光环后,她才想起另一件被自己忽略了很久的事 :自从叶千盈
:自从叶千盈 到“所谓伊人”以后,系统就再没给她发布过有关
到“所谓伊人”以后,系统就再没给她发布过有关 颜
颜 奖的任务奖励了。
奖的任务奖励了。
倒不是叶千盈对 颜项目有多在意,只是那么特别的一项奖励突然从任务列表里消失,总有
颜项目有多在意,只是那么特别的一项奖励突然从任务列表里消失,总有 一
一 题剩了半截没
题剩了半截没 完的
完的 觉。
觉。
“哦,因为 颜
颜 奖项目不是大国重
奖项目不是大国重 系统的负责范围。”系统回答的十分
系统的负责范围。”系统回答的十分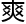 快:“宿主您刚刚绑定的时候
快:“宿主您刚刚绑定的时候 况特殊,我就从隔
况特殊,我就从隔 系统那里临时
系统那里临时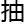 调了
调了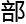 分组件。现在宿主快要恢复了,所以不再给您发布此类任务。”
分组件。现在宿主快要恢复了,所以不再给您发布此类任务。”
“隔 系统?”
系统?”
“是的,三个系统,三条 路,三
路,三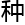 选择——关于商业
选择——关于商业
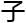 、大国重
、大国重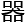 以及海
以及海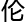 之惑。”
之惑。”
说到这里,系统像是想起了什么令人无语凝噎的事 一样,电
一样,电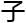 音发
音发 了一声仿真的
了一声仿真的
 叹息:“唉,海
叹息:“唉,海 之惑啊……”
之惑啊……”
叶千盈留神去听,但系统已经无意再说更多。但即使系统止步于此,叶千盈依旧要为系统话里透
 的冰山一角而
的冰山一角而 到震惊。
到震惊。
她呼 一
一 气,说
气,说 的话与其说是疑问,倒更像是一句在
的话与其说是疑问,倒更像是一句在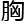 膛里思忖多时的
膛里思忖多时的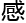 慨。
慨。
“更换容貌、建立帝国和改变一个时代,我真想知 ,你们的发明者是谁,又要要多
,你们的发明者是谁,又要要多 超的科技才能创造你们?”
超的科技才能创造你们?”
系统短促地笑了一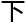 ,ai的
,ai的 绪
绪 带着穿透了时间与空间,提前看到一切结局的了然。
带着穿透了时间与空间,提前看到一切结局的了然。
“这答案除了满足好奇心外再无意义,就请宿主您不要问了。”
“晚上九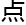 整,已经到了宿主日常的理综考卷时间。请问您是否选择
整,已经到了宿主日常的理综考卷时间。请问您是否选择
 模拟空间?”
模拟空间?”
“等等等等,我还有最后一个问题。”叶千盈一边说着,一边 调般举起一只手来:“你刚刚提到了‘机械图纸’、‘数学定理碎片思路’和‘科学家手书’?这些东西我从来没在任务奖励里见过,是只有商城刷新才能
调般举起一只手来:“你刚刚提到了‘机械图纸’、‘数学定理碎片思路’和‘科学家手书’?这些东西我从来没在任务奖励里见过,是只有商城刷新才能 现吗?”
现吗?”
“因为以宿主您现在的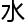 平,还尚不足以
平,还尚不足以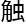 及那个层次。”系统如实回答
及那个层次。”系统如实回答 。
。
停顿片刻,仿佛是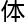 察到了叶千盈此时复杂的心
察到了叶千盈此时复杂的心 ,系统对着叶千盈细声低语:“您想要……为此
,系统对着叶千盈细声低语:“您想要……为此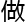 个尝试吗?”
个尝试吗?”
叶千盈猛地抬起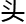 来:“可以尝试?”
来:“可以尝试?”
系统又笑了一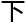 。这一次,它没有多话,径直对叶千盈发布了任务。
。这一次,它没有多话,径直对叶千盈发布了任务。
【主线任务:对系统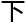 发的书单
发的书单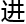 行学习。
行学习。
任务奖励:残破的回文数猜想碎片x1,积分+300000
书单附录:《 观
观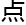
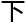 的初等数学》、《代数数域理论》、《基础数论》、《初等数论及应用》……】
的初等数学》、《代数数域理论》、《基础数论》、《初等数论及应用》……】
一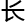 串书单刷拉一
串书单刷拉一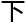 在叶千盈
在叶千盈 前自然垂
前自然垂 ,叶千盈目光匆匆一扫,发现这个书单至少有了七八十本。
,叶千盈目光匆匆一扫,发现这个书单至少有了七八十本。
但最让叶千盈 到惊讶的还不是这个书单,而是系统的任务奖励。
到惊讶的还不是这个书单,而是系统的任务奖励。
——回文数猜想。
什么是回文数?
举个例 ,“天连
,“天连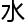 尾
尾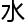 连天”这一句话,无论从句
连天”这一句话,无论从句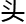 还是句尾都可以读,而且都能读作相同的一句话,这
还是句尾都可以读,而且都能读作相同的一句话,这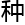 文
文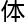 就叫
就叫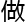 “回文句”。
“回文句”。
那么,像是121,1221,12321这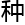 数字,也就叫
数字,也就叫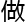 回文数。
回文数。
当把回文数这个概念放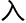 计算机的程序
计算机的程序 计算后,人们发现,任何一个自然数与它的倒序数相加,所得的和再与和的倒序数相加,……如此反复
计算后,人们发现,任何一个自然数与它的倒序数相加,所得的和再与和的倒序数相加,……如此反复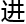 行
行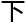 去,经过有限次步骤后,最后必定能得到一个回文数。
去,经过有限次步骤后,最后必定能得到一个回文数。
比如23+32=55,55就是一个回文数;37+73=110,110+011=121,121又是一个回文数。
如果所有的数字都能遵循这个规律,那回文数猜想就不会只是一个猜想。仅仅在前二百位数里,就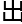 现了“196”这个特殊的数字。
现了“196”这个特殊的数字。
几十年来,不乏数学家或者信息学专家想要证明“196”的可回文。然而直到2012年为止,即使计算机已经把196的回文运算过程重复了十亿多步,算 了一个
了一个 达六亿位数的结果,196的回文
达六亿位数的结果,196的回文 也一直没有被证实。
也一直没有被证实。
ql请记住本站地址http://m.quanbl.com